Clip If the variance of the population is 10, what is the variance of the sampling distribution ?

Mẹo về If the variance of the population is 10, what is the variance of the sampling distribution Chi Tiết

Bùi Thanh Tùng đang tìm kiếm từ khóa If the variance of the population is 10, what is the variance of the sampling distribution được Cập Nhật vào lúc : 2022-10-25 03:00:12 . Với phương châm chia sẻ Thủ Thuật về trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi Read Post vẫn ko hiểu thì hoàn toàn có thể lại phản hồi ở cuối bài để Tác giả lý giải và hướng dẫn lại nha.

Consider a population that is finite, and sampling is with replacement. If the variance of the population is 2176.8 with a sample size of 16, then the variance of the sampling distribution of means is:

137.04135.21136.05134.12 Nội dung chính Show

Consider a population that is finite, and sampling is with replacement. If the variance of the population is 2176.8 with a sample size of 16, then the variance of the sampling distribution of means is:Answer (Detailed Solution Below)22. If the variance of the population is 10, what is the variance of the sampling distribution of the means of size 5 drawn from this population? A.2 C. 1.41 B. 4.47 D.10 23. Which sample size will give a smaller standard error of the mean? A.12 C.25 B.20 D.35 24. What is the finite population correction factor if the size of the population is 200 and the sample size is 25? A. 0.979 C.0.938 B.0.879 D.0.856Gauthmathier2837How do you find the variance of a sample variance?How do you find the variance of a distribution?What is the variance of the sampling?

Answer (Detailed Solution Below)

Option 3 : 136.05

Free

Electric charges and coulomb's law (Basic)

10 Questions 10 Marks 10 Mins

Given:

The variance of the population (σ2) = 2176.8;

Sample size (N) = 16

Concept:

The variance of the sampling distribution of the mean is computed as follows:

(σ _M^2=fracσ ^2N)      

That is, the variance of the sampling distribution of the mean is the population variance divided by N, the sample size (the number of scores used to compute a mean). Thus, the larger the sample size, the smaller the variance of the sampling distribution of the mean.

Calculation:

We know that the variance of the sampling distribution of the mean is computed as follows:

(σ _M^2=fracσ ^2N)

(Rightarrow sigma _M^2=frac2176.816)

(Rightarrow sigma _M^2=136.05)

Hence, The variance of the sampling distribution of means is 136.05.

Last updated on Sep 29, 2022

Union Public Service Commission (UPSC) has released the NDA Result II 2022 (Name Wise List) for the exam that was held on 4th September 2022. Earlier, the roll number wise list was released by the board. A total number of 400 vacancies will be filled for the UPSC NDA II 2022 exam. The selection process for the exam includes a Written Exam and SSB Interview. Candidates who get successful selection under UPSC NDA II will get a salary range between Rs. 15,600 to Rs. 39,100.

22. If the variance of the population is 10, what is the variance of the sampling distribution of the means of size 5 drawn from this population? A.2 C. 1.41 B. 4.47 D.10 23. Which sample size will give a smaller standard error of the mean? A.12 C.25 B.20 D.35 24. What is the finite population correction factor if the size of the population is 200 and the sample size is 25? A. 0.979 C.0.938 B.0.879 D.0.856

Question

Gauthmathier2837

Grade 10 · 2022-06-27

YES! We solved the question!

Check the full answer on App Gauthmath

22. If the variance of the population is 22. If the variance of the population is 10, what - Gauthmath, what is the variance of the sampling distribution of the means of size 5 drawn from this population?
A. 2
C. 1.41
B. 4.47
D. 10 23. Which sample size will give a smaller standard error of the mean?
A. 12
C. 25
B. 20
D. 35 24. What is the finite population correction factor if the size of the population is 200 and the sample size is 25?
A. 0.979
C. 0.938
B. 0.879 D. 0.856

Vicki

Answer

Explanation

Thanks (179)

Feedback from students

Does the answer help you? Rate for it!

Still have questions?
Ask a live tutor for help now.

Enjoy live Q.&A or pic answer.

Provide step-by-step explanations.

Unlimited access to all gallery answers.

(X_1, X_2, ldots, X_n)are observations of a random sample of size (n) from the normal distribution (N(mu, sigma^2))(barX=dfrac1nsumlimits_i=1^n X_i) is the sample mean of the (n) observations, and(S^2=dfrac1n-1sumlimits_i=1^n (X_i-barX)^2) is the sample variance of the (n) observations.

Then:

(barX)and (S^2) are independent(dfrac(n-1)S^2sigma^2=dfracsum_i=1^n (X_i-barX)^2sigma^2sim chi^2(n-1))

Proof

The proof of number 1 is quite easy. Errr, actually not! It is quite easy in this course, because it is beyond the scope of the course. So, we'll just have to state it without proof.

Now for proving number 2. This is one of those proofs that you might have to read through twice... perhaps reading it the first time just to see where we're going with it, and then, if necessary, reading it again to capture the details. We're going to start with a function which we'll call (W):

(W=sumlimits_i=1^n left(dfracX_i-musigmaright)^2)

Now, we can take (W) and do the trick of adding 0 to each term in the summation. Doing so, of course, doesn't change the value of (W):

(W=sumlimits_i=1^n left(dfrac(X_i-barX)+(barX-mu)sigmaright)^2)

As you can see, we added 0 by adding and subtracting the sample mean to the quantity in the numerator. Now, let's square the term. Doing just that, and distributing the summation, we get:

(W=sumlimits_i=1^n left(dfracX_i-barXsigmaright)^2+sumlimits_i=1^n left(dfracbarX-musigmaright)^2+2left(dfracbarX-musigma^2right)sumlimits_i=1^n (X_i-barX))

But the last term is 0:

(W=sumlimits_i=1^n left(dfracX_i-barXsigmaright)^2+sumlimits_i=1^n left(dfracbarX-musigmaright)^2+ underbrace 2left(dfracbarX-musigma^2right)sumlimits_i=1^n (X_i-barX)_0, since sum(X_i - barX) = nbarX-nbarX=0)

so, (W) reduces to:

(W=sumlimits_i=1^n dfrac(X_i-barX)^2sigma^2+dfracn(barX-mu)^2sigma^2)

We can do a bit more with the first term of (W). As an aside, if we take the definition of the sample variance:

(S^2=dfrac1n-1sumlimits_i=1^n (X_i-barX)^2)

and multiply both sides by ((n-1)), we get:

((n-1)S^2=sumlimits_i=1^n (X_i-barX)^2)

So, the numerator in the first term of (W) can be written as a function of the sample variance. That is:

(W=sumlimits_i=1^n left(dfracX_i-musigmaright)^2=dfrac(n-1)S^2sigma^2+dfracn(barX-mu)^2sigma^2)

Okay, let's take a break here to see what we have. We've taken the quantity on the left side of the above equation, added 0 to it, and showed that it equals the quantity on the right side. Now, what can we say about each of the terms. Well, the term on the left side of the equation:

(sumlimits_i=1^n left(dfracX_i-musigmaright)^2)

is a sum of (n) independent chi-square(1) random variables. That's because we have assumed that (X_1, X_2, ldots, X_n)are observations of a random sample of size (n) from the normal distribution (N(mu, sigma^2)). Therefore:

(dfracX_i-musigma)

follows a standard normal distribution. Now, recall that if we square a standard normal random variable, we get a chi-square random variable with 1 degree of freedom. So, again:

(sumlimits_i=1^n left(dfracX_i-musigmaright)^2)

is a sum of (n) independent chi-square(1) random variables. Our work from the previous lesson then tells us that the sum is a chi-square random variable with (n) degrees of freedom. Therefore, the moment-generating function of (W) is the same as the moment-generating function of a chi-square(n) random variable, namely:

(M_W(t)=(1-2t)^-n/2)

for (t

(dfracn(barX-mu)^2sigma^2)

is a chi-square(1) random variable. That's because the sample mean is normally distributed with mean (mu) and variance (fracsigma^2n). Therefore:

(Z=dfracbarX-musigma/sqrtnsim N(0,1))

is a standard normal random variable. So, if we square (Z), we get a chi-square random variable with 1 degree of freedom:

(Z^2=dfracn(barX-mu)^2sigma^2sim chi^2(1))

And therefore the moment-generating function of (Z^2) is:

(M_Z^2(t)=(1-2t)^-1/2)

for (t

Now, let's use the uniqueness property of moment-generating functions. By definition, the moment-generating function of (W) is:

(M_W(t)=E(e^tW)=Eleft[e^t((n-1)S^2/sigma^2+Z^2)right])

Using what we know about exponents, we can rewrite the term in the expectation as a product of two exponent terms:

(E(e^tW)=Eleft[e^t((n-1)S^2/sigma^2)cdot e^tZ^2right]=M_(n-1)S^2/sigma^2(t) cdot M_Z^2(t))

The last equality in the above equation comes from the independence between (barX) and (S^2). That is, if they are independent, then functions of them are independent. Now, let's substitute in what we know about the moment-generating function of (W) and of (Z^2). Doing so, we get:

((1-2t)^-n/2=M_(n-1)S^2/sigma^2(t) cdot (1-2t)^-1/2)

Now, let's solve for the moment-generating function of (frac(n-1)S^2sigma^2), whose distribution we are trying to determine. Doing so, we get:

(M_(n-1)S^2/sigma^2(t)=(1-2t)^-n/2cdot (1-2t)^1/2)

Adding the exponents, we get:

(M_(n-1)S^2/sigma^2(t)=(1-2t)^-(n-1)/2)

for (t

(dfrac(n-1)S^2sigma^2=dfracsumlimits_i=1^n (X_i-barX)^2sigma^2 sim chi^2_(n-1))

as was to be proved! And, to just think that this was the easier of the two proofs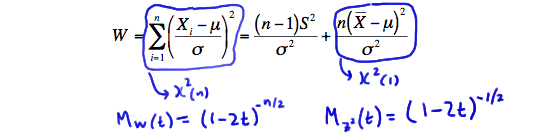

How do you find the variance of a sample variance?

The steps to find the sample variance are as follows:. Find the mean of the data.. Subtract the mean from each data point.. Take the summation of the squares of values obtained in the previous step.. Divide this value by n - 1..

How do you find the variance of a distribution?

To find the variance σ2 of a discrete probability distribution, find each deviation from its expected value, square it, multiply it by its probability, and add the products. To find the standard deviation σ of a probability distribution, simply take the square root of variance σ2.

What is the variance of the sampling?

Sampling variance is the variance of the sampling distribution for a random variable. It measures the spread or variability of the sample estimate about its expected value in hypothetical repetitions of the sample. Tải thêm tài liệu liên quan đến nội dung bài viết If the variance of the population is 10, what is the variance of the sampling distribution

Video If the variance of the population is 10, what is the variance of the sampling distribution ?

Bạn vừa Read tài liệu Với Một số hướng dẫn một cách rõ ràng hơn về Clip If the variance of the population is 10, what is the variance of the sampling distribution tiên tiến nhất

Chia Sẻ Link Cập nhật If the variance of the population is 10, what is the variance of the sampling distribution miễn phí

Heros đang tìm một số trong những Chia Sẻ Link Cập nhật If the variance of the population is 10, what is the variance of the sampling distribution miễn phí.

Giải đáp thắc mắc về If the variance of the population is 10, what is the variance of the sampling distribution

Nếu sau khi đọc nội dung bài viết If the variance of the population is 10, what is the variance of the sampling distribution vẫn chưa hiểu thì hoàn toàn có thể lại Comment ở cuối bài để Tác giả lý giải và hướng dẫn lại nha #variance #population #variance #sampling #distribution - 2022-10-25 03:00:12 If the variance of the population is 10, what is the variance of the sampling distribution