Clip Cách giải bất phương trình bậc 2 bằng máy tính 580 ?
Mẹo Hướng dẫn Cách giải bất phương trình bậc 2 bằng máy tính 580 Mới Nhất
Bùi Khánh Ngọc đang tìm kiếm từ khóa Cách giải bất phương trình bậc 2 bằng máy tính 580 được Update vào lúc : 2022-06-09 05:05:06 . Với phương châm chia sẻ Thủ Thuật Hướng dẫn trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi tham khảo tài liệu vẫn ko hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Admin lý giải và hướng dẫn lại nha.
Tương ứng với giải phương trình là giải bất phương trình. Tính năng nổi trội: giải bất phương trình bậc bốn. Bài toán: giải bất phương trình: $-x^4+5x^3-5x^2-5x+6 geq 0$.Bài Viết Tương Tự1 Giải bất phương trình2 Nghiệm đặc biệt khi giải bất phương trìnhVideo liên quan
[embed]https://www.youtube.com/watch?v=lUws0ljQLEk[/embed]
Ở đây ta sẽ sử dụng MT CASIO FX-570 VN PLUS
(1): Ấn nút mode
(2): Ấn nút mũi tên chỉ xuống
(Bước 3): Ấn số 1
(4): Ấn tiếp số 1 để chọn bậc của BPT
(5): Ấn số 4 để chọn dạng BPT
Sau khi chọn chính sách giải bất phương trình số 1 một ẩn rồi thì ta thay thông số của bất phương trình cần giải vào và ấn dấu "=”
Ví dụ:
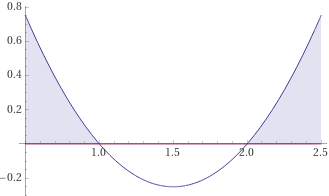
Giải bất phương trình $7x^2-10x-9 le 0$
Lưu ý: Phải xác định đúng những thông số $a,b,c$.
1.2.7 Chức năng giải bất phương trình wz(A)
Menu A
giải những bất phương trình từ bậc hai đến bậc bốn, đặc biệt là bất phương trình bậc bốn. Đối với bậc Trung học cơ sở, menu này ít khi được dùng đến vì những bất phương trình đa phần dạy cho những học viên từ lớp 10 trở lên, do đó những em sẽ có thời cơ sử dụng nó lên học lên bậc học Trung học phổ thông. wz(A)
Ví dụ 7 Giải bất phương trình: [latex]large x^4-4x^3+3x^2+8x-10leq 0[/latex]
wx(B) 
1=z4=3=8=z10=
Tuy máy tính đã xuất ra nghiệm của bất phương trình bậc bốn, tuy nhiên muốn trình bày lời giải bằng tự luận, ta phải gia công thêm như sau:
Lưu ý: Ta Dự kiến [latex]large pm sqrt2[/latex] là nghiệm của phương trình bậc bốn nên đa thức chia hết cho [latex]large x^2-2[/latex]
[latex]large 996|005rightarrow 1|-4|5[/latex]
Lưu ý: Ngoài phương pháp “CALC 1000” như trên để tìm thương, ta hoàn toàn có thể nhận thấy ngay thông số bậc hai là một trong và thông số tự do là 5. Để tìm thông số số 1 là hoàn toàn có thể thực hiện như sau:
Giải. Bất phương trình đã cho tương đương với
[latex]large (x^2-2)(x^2-4x+5)leq 0Leftrightarrow -sqrt2leq xleq sqrt2[/latex](Còn tiếp)
Bài Viết Tương Tự
SỬ DỤNG TÍNH NĂNG BẢNG GIÁ TRỊ TABLE Phương pháp: $lozenge$ Nhấn $lozenge$ $f(x)=$ nhập …
Phương thức Inequality được cho phép tất cả chúng ta giải bất phương trình bậc 2, bậc 3 và bậc 4. Tất cả những dấu
của bất phương trình điều được tương hỗ Về cách giải bất phương trình số 1 bằng Casio fx-580VN X mình vẫn đang nghiên cứu và phân tích. Tuy đã giải được một lớp khá lớn nhưng vẫn chưa hoàn thiện, lúc nào hoàn thiện mình sẽ ra mắt với những bạn
Xem thêm Giải bất phương trình số 1 một ẩn bằng máy tính Casio fx-580VN X
1 Giải bất phương trình
Giải bất phương trình
Bước 1 Nhấn phím MENU
Bước 2 Nhấn phím A để chọn phương thức Inequality
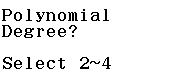
Bước 3 Chọn bậc của bất phương trình
Vì cần giải bất phương trình bậc 2 nên mình sẽ nhấn phím 2
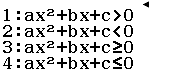
Bước 4 Chọn dấu của bất phương trình
Vì cần chọn dấu
nên mình sẽ nhấn phím 1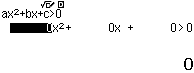 
Bước 5 Nhập thông số thứ nhất => nhấn phím = => … => nhập thông số ở đầu cuối => nhấn phím =
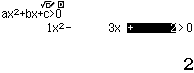
Bước 6 Nhấn phím =
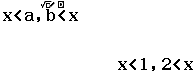
Vậy tập nghiệm của bất phương trình đã cho là
Giải bất phương trình
Bước 1 Nhấn phím OPTN
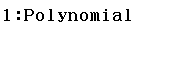
Bước 2 Nhấn phím 1 để chọn Polynomial
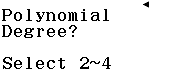
Bước 3 Chọn bậc của bất phương trình
Vì cần giải bất phương trình bậc 3 nên mình sẽ nhấn phím 3
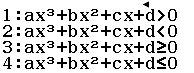
Bước 4 Chọn dấu của bất phương trình
Vì cần chọn dấu
nên mình sẽ nhấn phím 2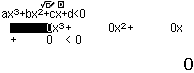 
Bước 5 Nhập thông số thứ nhất => nhấn phím = => … => nhập thông số ở đầu cuối => nhấn phím =
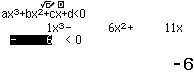
Bước 6 Nhấn phím =
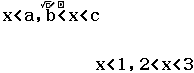
Vậy tập nghiệm của bất phương trình đã cho là
Giải bất phương trình
Bước 1 Chọn bất phương trình bậc bốn và dấu
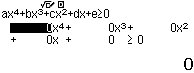
Bước 2 Nhập những thông số tương ứng
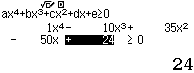
Bước 3 Nhấn phím =
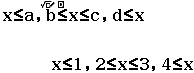
Vậy tập nghiệm của bất phương trình đã cho là
2 Nghiệm đặc biệt khi giải bất phương trình
- All Real Numbers bất phương trình đã cho có vô số nghiệmNo Solution bất phương trình đã cho vô nghiệm
