Hướng Dẫn Tính diện tích s của hình phẳng giới hạn bởi đồ thị hàm số y = x trục hoành và đường thẳng x = -4 ?
Kinh Nghiệm về Tính diện tích s quy hoạnh s của hình phẳng số lượng giới hạn bởi đồ thị hàm số y = x trục hoành và đường thẳng x = -4 Mới Nhất
Lê Hữu Kông đang tìm kiếm từ khóa Tính diện tích s quy hoạnh s của hình phẳng số lượng giới hạn bởi đồ thị hàm số y = x trục hoành và đường thẳng x = -4 được Update vào lúc : 2022-05-18 14:20:07 . Với phương châm chia sẻ Bí quyết về trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi Read tài liệu vẫn ko hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Ad lý giải và hướng dẫn lại nha.
Or you want a quick look:
Nội dung chính- Tính diện tích s quy hoạnh hình phẳng số lượng giới hạn bởi đồ thị hàm số , trục hoành và hai tuyến đường thẳng ,.
Bài tập trắc nghiệm 45 phút Ứng dụng tích phân trong bài toán thực tế (cho sẵn hàm số) - Toán Học 12 - Đề số 15Video liên quan
I - Diện tích hình phẳng
1. Diện tích hình phẳng số lượng giới hạn bởi một đồ thị hàm số
Hàm số y = f(x) liên tục trên đoạn [a ; b] thì diện tích s quy hoạnh S của hình phẳng số lượng giới hạn bởi đồ thị hàm số f(x),
trục hoành và hai tuyến đường thẳng có phương trình x = a, x = b được tính bằng công thức:
S =
|f(x)| dx
Do đó để tính S ta hoàn toàn có thể thực hiện :
a) Hoặc xét dấu biểu thức f(x) trên đoạn [a ; b] để khử giá trị tuyệt đối.
b) Hoặc giải phương trình f(x) = 0 và phân biệt:
* Trường hợp f(x) = 0 vô nghiệm trên đoạn [a ; b] tức (C) : y = f(x) không cắt Ox trên đoạn [a ; b].Ta chỉ việc tính:
f(x)dx và khi đó:
* Trường hợp f(x) = 0 có nghiệm trên đoạn [a ; b], giả sử là α, β (α <β), tức (C) : y = f(x) cắt Ox tại hai
điểm có x = α, x = β trên đoạn [a ; b].
Ta chỉ việc tính một nguyên hàm F(x) của f(x) và khi đó:
2. Trường hợp hình phẳng số lượng giới hạn bởi hai đô thị hàm số
Diện tích hình phẳng số lượng giới hạn bởi hai đồ thị hàm số y = f(x), y = g(x) và hai tuyến đường thẳng có phương trình
x= a, x = b được tính bởi công thức:
S =
|f(x) - g(x)|dx
Do đó để tính S ta hoàn toàn có thể thực hiện:
a) Hoặc xét dấu biểu thức [f(x) - g(x)] để khử giá trị tuyệt đối.
b) Hoặc giải phương trình f(x) - g(x) = 0 và phân biệt:
* Trường hợp f(x) - g(x) = 0 vô nghiệm trên [a ; b], tức đồ thị của hai hàm số không cắt nhau trên đoạn
[a ; b]. Ta chỉ việc tính
[f(x) - g(x)]dx, khi đó:
* Trường hợp f(x) - g(x) = 0 có nghiệm trên đoạn [a ; b], giả sử là c, d (c < d), tức đồ thị của hai hàm số
y = f(x), y = g(x) cắt nhau tại hai điểm có x = c, x = d trên đoạn [a ; b].
Ta tính một nguyên hàm của f(x) - g(x) là F(x) - G(x) và có:
Ghi chú:
* Nếu phải tính diện tích s quy hoạnh hình phẳng số lượng giới hạn bởi ba đồ thị hàm số trở lên, ta phải vẽ hình và chia hình
phẳng phải tìm diện tích s quy hoạnh thành nhiều hình phẳng nhỏ được số lượng giới hạn bởi hai tuyến đường.
* Một số trường hợp tính diện tích s quy hoạnh hình phẳng, ta hoàn toàn có thể chuyển đổi biểu thức hàm số thành x theo y, lấy
tích phân theo biến số y để bài toán được đơn giản hơn.
II- Thể tích vật thể
1. Thể tích của vật thể
Trong không khí Oxy, cho một vật thể B được số lượng giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại x= a,
x = b và có S(x) là diện tích s quy hoạnh thiết diện bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ
x ∈ [a ; b], nếu S = S(x) là hàm số liên tục trên đoạn [a ; b] thì thể tích V của vật thể B được tính bằng
công thức:
V =
2. Thể tích khối tròn xoay
Hình phẳng số lượng giới hạn bởi đồ thị (C): y = f(x) (liên tục và không âm trên đoạn [a ; b]), trục hoành và
hai đường thẳng x = a, x = b quay quanh trục hoành tạo nên một khối tròn xoay hoàn toàn có thể tích được tính
theo công thức:
Tương tự nếu đồ thị (C): x = g(y) liên tục trên đoạn [c ; d]). Hình phẳng số lượng giới hạn bởi (C): x = g(y), trục
tung và hai đường thẳng y = c, y = d, quay quanh trục tung tạo nên một khối tròn xoay hoàn toàn có thể tích V được
tính theo công thức:
Ví dụ:
Diện tích hình phẳng số lượng giới hạn bởi đồ thị (P): y = -x2 + 2x - 1, trục Ox và hai đường thẳng x =1, x = 3 là:
A. 3 (đvdt) B.
(đvdt) C. 
D. 
Giải
Ta có: y = -x2 + 2x - 1 < 0, ∀x ∈ R. y = x2 - 2x + 1 = 0 có nghiệm duy nhất x = 1, nên diện tích s quy hoạnh hình phẳng số lượng giới hạn bởi (P), trục Ox và hai đường thẳng x = 1; x = 3 là:
Chọn phương án C.
Hoặc ta hoàn toàn có thể trình bày lời giải như sau: phương trình f(x) = 0 có một nghiệm duy nhất x = 1 ∈ [1 ; 3] nên:
See more articles in the category: BLOG ĐIỆN TỬ
0
Chương 3: Nguyên Hàm - Tích Phân Và Ứng Dụng
Tính diện tích s quy hoạnh hình phẳng số lượng giới hạn bởi đồ thị hàm số y = ex - e-x , trục hoành, đường thẳng x = -1 và đường thẳng x = 1.
Phương pháp giải:
- Giải phương trình hoành độ giao điểm, tìm những nghiệm.
- Diện tích hình phẳng số lượng giới hạn bởi đồ thị hàm số (y = fleft( x right)), trục hoành, đường thẳng (x = a,,,x = b) là (S = intlimits_a^b fleft( x right) right ).
Giải rõ ràng:
Xét phương trình hoành độ giao điểm: (x^5 - x^3 = 0 Leftrightarrow x^3left( x^2 - 1 right) = 0 Leftrightarrow left[ beginarraylx = 0\x = pm 1endarray right.).
(beginarrayl Rightarrow S = intlimits_ - 1^0 dx + intlimits_0^1 dx \,,,,,,S = left| intlimits_ - 1^0 left( x^5 - x^3 right)dx right| + left| intlimits_0^1 left( x^5 - x^3 right)dx right|\,,,,,,S = dfrac112 + dfrac112 = dfrac16endarray)
Chọn C.
Trang chủ
Sách ID
Khóa học miễn phí
Luyện thi ĐGNL và ĐH 2023
Tính diện tích s quy hoạnh hình phẳng số lượng giới hạn bởi đồ thị hàm số , trục hoành và hai tuyến đường thẳng ,.
A.
B.
C.
D.
Đáp án và lời giải
Đáp án:C
Lời giải:
.
Vậy đáp án đúng là C.
Câu hỏi thuộc đề thi sau. Bạn có mong ước thi thử?
Bài tập trắc nghiệm 45 phút Ứng dụng tích phân trong bài toán thực tế (cho sẵn hàm số) - Toán Học 12 - Đề số 15
Làm bài
Chia sẻ
Một số thắc mắc khác cùng bài thi.
Cho hình phẳng H giới hạn bởi đường parabol P: y=x2−x+2 và tiếp tuyến của đồ thị hàm số y=x2+1 tại điểm có tọa độ 1;2 . Diện tích của hình H là
Thể tích khối tròn xoay sinh ra khi quay hình phẳng số lượng giới hạn bởi những đường
và 
quanh trục Oxgần nhất với giá trị nào sau đây:
Trong một mẻ cấy, số lượng ban đầu của vi khuẩn là 500, số lượng này tăng lên theo vận tốc
vi khuẩn trong 1 giờ. Sẽ có bao nhiêu vi khuẩn trong buồng cấy sau 3 giờ?
Diện tích của hình phẳng số lượng giới hạn bởi đồ thị hàm số y=x , trục hoành và đường thẳng y=x−2 là
Một lực có độ lớn 40 N (newton) thiết yếu để kéo căng một chiếc lò xo có độ dài tự nhiên 10 cm lên 15 cm. Biết rằng theo định luật
trong Vật lý, khi một chiếc lò xo bị kéo căng thêm 
(đơn vị độ dài) so với độ dài tự nhiên của lò xo thì lò xo trì lại (chống lại) với một lực cho bởi công thức 
, trong đó 
là thông số đàn hồi (hoặc độ cứng) của lò xo. Hãy tìm công sinh ra khi kéo lò xo có độ dài từ 15 cm đến 20 cm ? (kí hiệu 
là đơn vị của công).
Một xe máy đang chạy với vận tốc 8 m/s thì tài xế đạp phanh; từ thời điểm đó, xe máy hoạt động và sinh hoạt giải trí chậm dần đều với vận tốc
, trong đó t là khoảng chừng thời gian tính bằng giây, Tính từ lúc lúc đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, xe máy còn di tán được bao nhiêu mét ?
Một đám vi trùng ngày thứ
có số lượng là 
. Biết rằng 
và lúc đầu đám vi trùng có 250.000 con. Sau 10 ngày số lượng vi trùng là (lấy xấp xỉ hàng đơn vị):
Parabol P:y=12x2 chia hình tròn trụ số lượng giới hạn bởi đường tròn C:x2+y2=8 thành hai phần như hình vẽ. Gọi S1 là diện tích s quy hoạnh của phần tô đậm và S2 là diện tích s quy hoạnh của phần không tô đậm. Tính S1S2
Tính diện tích s quy hoạnh hình phẳng số lượng giới hạn bởi đồ thị hàm số
, trục hoành và những đường thẳng 
.
Cho
là hình phẳng số lượng giới hạn bởi parabol 
, cung tròn có phương trình 
(với 
) và trục hoành (phần tô đậm trong hình vẽ). Diện tích của 
bằng:
Một chiếc xe thể thao hiệu Lamborghini Aventador chạy trên một đường đua thẳng có độ dài 4km. Xe tăng tốc từ 0km/h đến 100km/h trong 3 giây đầu tiên đi hết 260m và sau đó xe hoạt động và sinh hoạt giải trí nhanh dần đều với tần suất
. Tính thời gian để xe hoàn thành xong đường đua biết vận tốc của hoạt động và sinh hoạt giải trí nhanh dần đều có công thức 
với 
là tần suất và vận tốc đầu
Cho
và 
. Tính 
theo a và m.
Một ô tô đang chạy với vận tốc
thì gặp chướng ngại vật nên người lái xe đã đạp phanh. Từ thời điểm đó ô tô hoạt động và sinh hoạt giải trí chậm dần đều với tần suất 
trong đó là thời gian tính bằng giây, Tính từ lúc lúc khởi đầu đạp phanh. Biết từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di tán được 16m. Tính 
.
Tính diện tích s quy hoạnh hình phẳng số lượng giới hạn bởi đồ thị của những hàm số y=x2+2x+2,y=−x2+x+3 .
Gọi H là hình số lượng giới hạn bởi đồ thị những hàm số y=x , y=2−x và trục hoành. Diện tích của hình H bằng
Cho hình phẳng D được số lượng giới hạn bởi hai tuyến đường y=2(x2−1); y=1−x2. Tính thể tích khối tròn xoay tạo thành do D quay quanh trục Ox .
Hai người chạy đua xuất phát cùng lúc với vận tốc 0 m/s trên một đoạn đường 400m. Biết độ tăng vận tốc của 2 người lần lượt cho bởi hai hàm số
và 
(t là thời gian, tính theo giây). Hỏi thời gian về đích của hai người chênh lệch bao nhiêu giây?
Cho hàmsố
làhàmsốliêntụctrên
. Tìmkhẳngđịnhsai?
Cho (P)
và (d)
. Tìm m để diện tích s quy hoạnh hình phẳng số lượng giới hạn (P) và (d) đạt giá trị nhỏ nhất?
Tính diện tích s quy hoạnh S của hình phẳng số lượng giới hạn bởi đồ thị hàm số
trục hoành và hai tuyến đường thẳng 
Cho hàm số fx liên tục trên ℝ . Gọi S là diện tích s quy hoạnh hình phẳng số lượng giới hạn bởi những đường y=fx , y=0 , x=−1 và x=5 (như hình vẽ bên). Mệnh đề nào dưới đây đúng?
Tính diện tích s quy hoạnh hình phẳng số lượng giới hạn bởi đồ thị hàm số
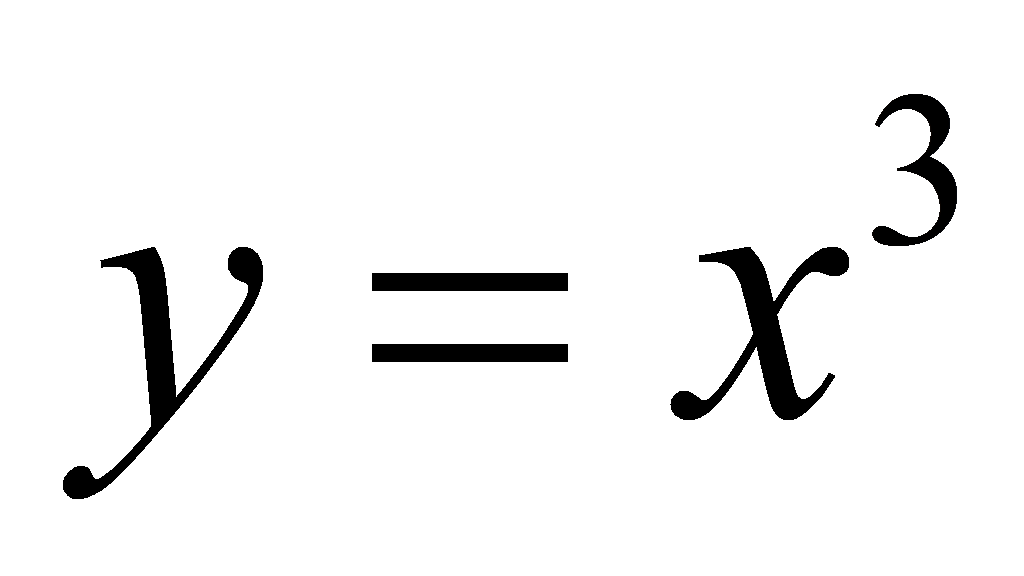, trục hoành và hai tuyến đường thẳng 
,
.
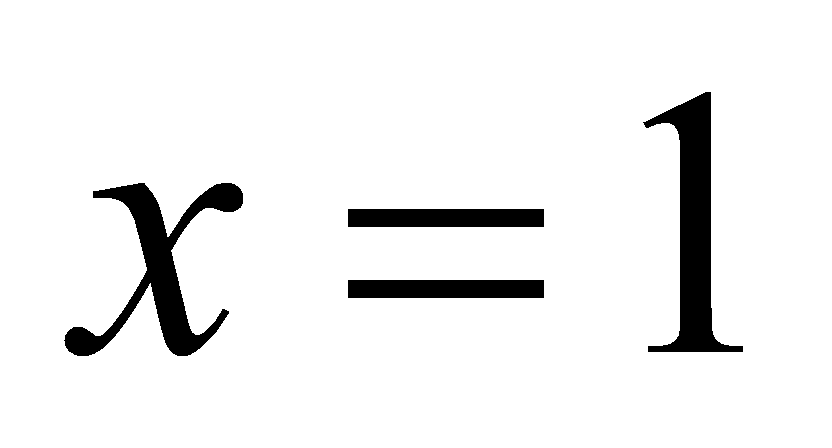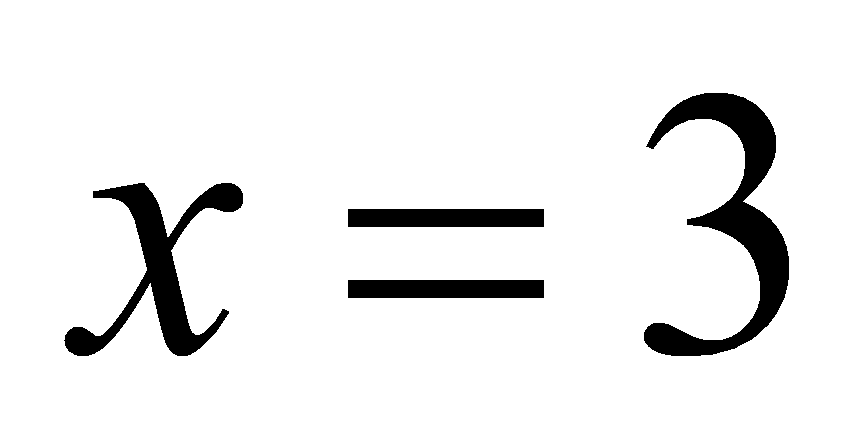Parabol
chia hai đường tròn có tâm tại gốc tọa độ, bán kính bằng 
thành 2 phần. Tỉ số diện tích của chúng thuộc khoảng nào trong các khoảng sau đây?
Hình phẳng số lượng giới hạn bởi những đường y=ex,y=0,x=0,x=ln5 có diện tích s quy hoạnh bằng
Cho hình phẳng H số lượng giới hạn bởi đồ thi những hàm số 
và 
, 
. Khi đó diện tích s quy hoạnh H là :
Một số thắc mắc khác hoàn toàn có thể bạn quan tâm.
Khi nói về đột biến gen, phát biểu nào sau đây không đúng?
Khi nói về đột biến gen, phát biểu nào sau đây không đúng? .
Loại đột biến nào sau đây hoàn toàn có thể làm tăng số loại alen của một gen trong vốn gen của quần thể?
Giả sử trong một gen có một bazo nito guanin trở thành dạng hiếm (G*). Khi gen này nhân đôi 3 lần thì số gen ở dạng tiền đột biến là:
Một đoạn của gen cấu trúc có trật tự nucleotit trên mạch gốc như sau: 3’TAX – AAG – GAG – AAT – GTT- TTA – XXT – XGG- GXG – GXX – GAA – ATT 5’ Nếu đột biến thay thế nuclêôtit thứ 19 là X thay bằng A, thì số axit amin (aa) môi trường tự nhiên thiên nhiên đáp ứng cho gen đột biến tổng hợp (Tính cả a.a mở đầu) là:
Khi nói về đột biến gen, phát biểu nào sau đây không đúng?
Khi nói về đột biến gen, có bao nhiêu phát biểu sau đây đúng?
I. Đột biến điểm là dạng đột biến mất thêm, thay thế nhiều cặp nucleotit.
II. Đột biến xuất hiện ở tế bào xôma, thì không di truyền qua sinh sản hữu tính.
III. Gen có cấu trúc bền vững thì rất dễ bị đột biến tạo thành nhiều alen mới.
IV. Đột biến xuất hiện ở giao tử thường di truyền cho thế hệ sau qua sinh sản hữu tính.
Một gen của sinh vật nhân sơ chỉ huy tổng hợp 3 polipeptit đã lôi kéo từ môi trường tự nhiên thiên nhiên nội bào 597 axit amin nhiều chủng loại. Phân tử mARN được tổng hợp từ gen trên có 100A ; 125U . Gen đã bị đột biến dẫn đến hậu quả tổng số nuclêôtit trong gen không thay đổi nhưng tỷ lệ A/G bị thay đổi và bằng 59,57%. Đột biến trên thuộc dạng nào sau đây?
Một gen có chiều dài 3060Ao, trong đó A = 3/7G. Sau đột biến, chiều dài gen không thay đổi và có tỉ lệ ≈ 42,18%. Số link hyđrô của gen đột biến là
Loại đột biến làm tăng số loại alen trong khung hình là:
