Video Cho hình lăng trụ đứng ABC A phẩy B phẩy C phẩy có đáy ABC là tam giác đều cạnh a 🆗
Mẹo về Cho hình lăng trụ đứng ABC A phẩy B phẩy C phẩy có đáy ABC là tam giác đều cạnh a Chi Tiết
Bùi Thị Vân Thiện đang tìm kiếm từ khóa Cho hình lăng trụ đứng ABC A phẩy B phẩy C phẩy có đáy ABC là tam giác đều cạnh a được Cập Nhật vào lúc : 2022-04-22 23:50:06 . Với phương châm chia sẻ Bí kíp về trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi Read Post vẫn ko hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Mình lý giải và hướng dẫn lại nha.Cho hình lăng trụ đứng (ABC.A'B'C' ) có đáy (ABC ) là tam giác vuông, (AB = BC = a. ) Biết rằng góc giữa hai mặt phẳng ((ACC') ) và ((AB'C') ) bằng ((60^0) ) (tham khảo hình vẽ bên). Thể tích của khối chóp (B'.ACC'A' ) bằng
Nội dung chính- Cho hình lăng trụ đứng (ABC.A'B'C' ) có đáy (ABC ) là tam giác vuông, (AB = BC = a. ) Biết rằng góc giữa hai mặt phẳng ((ACC') ) và ((AB'C') ) bằng ((60^0) ) (tham khảo hình vẽ bên). Thể tích của khối chóp (B'.ACC'A' ) bằng Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a, cạnh bên A’B tạo với đáy một góc 45. Thể tích khối lăng trụ ABC.A’B’C’ là:
Bài tập trắc nghiệm 60 phút Thể tích khối lăng trụ. - Khối đa diện và thể tích - Toán Học 12 - Đề số 9Video liên quan
Câu 33733 Vận dụng cao
Cho hình lăng trụ đứng (ABC.A'B'C') có đáy (ABC) là tam giác vuông, (AB = BC = a.) Biết rằng góc giữa hai mặt phẳng ((ACC')) và ((AB'C')) bằng (60^0) (tham khảo hình vẽ bên). Thể tích của khối chóp (B'.ACC'A') bằng
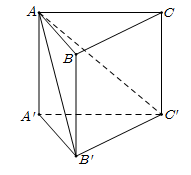
Đáp án đúng: a
Phương pháp giải
$V_B'.ACC'A' = V - V_B'.BAC = dfrac23V$, với V là thể tích khối lăng trụ.
Tính thể tích khối lăng trụ.
...Phương pháp giải:
Thể tích khối lăng trụ: (V = Sh).
Lời giải rõ ràng:
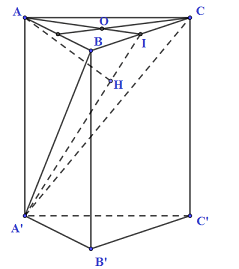
Gọi I là trung điểm cua BC, kẻ (AH bot A'I).
(Delta ABC) đều cạnh a ( Rightarrow AI = dfracasqrt 3 2;,,S_ABC = dfraca^2sqrt 3 4)
Ta có: (left{ beginarraylAI cap left( A'BC right) = left I right\AI = 3.OIendarray right. Rightarrow dleft( O;left( A'BC right) right) = dfrac13dleft( A;left( A'BC right) right))
Ta có: (left{ beginarraylBC bot AI\BC bot AA'endarray right. Rightarrow BC bot left( AA'I right) Rightarrow BC bot AH)
Mà (AH bot A'I Rightarrow AH bot left( A'BC right) Rightarrow dleft( A;left( A'BC right) right) = AH)
( Rightarrow dleft( O;left( A'BC right) right) = dfrac13AH = dfraca6 Rightarrow AH = dfraca2)
(Delta AA'I) vuông tại A, (AH bot A'I)
( Rightarrow dfrac1AH^2 = dfrac1AI^2 + dfrac1AA'^2 Leftrightarrow dfrac1left( dfraca2 right)^2 = dfrac1left( dfracasqrt 3 2 right)^2 + dfrac1AA'^2)
( Leftrightarrow dfrac4a^2 = dfrac43a^2 + dfrac1AA'^2)( Leftrightarrow AA' = dfracasqrt 6 4)
Thể tích khối lăng trụ ABC.A’B’C’ là: (V = S_ABC.AA' = dfraca^2sqrt 3 4.dfracasqrt 6 4 = dfrac3a^3sqrt 2 16).
Chọn: A
Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a, cạnh bên A’B tạo với đáy một góc 45. Thể tích khối lăng trụ ABC.A’B’C’ là:
A.
![]() .
.
B.
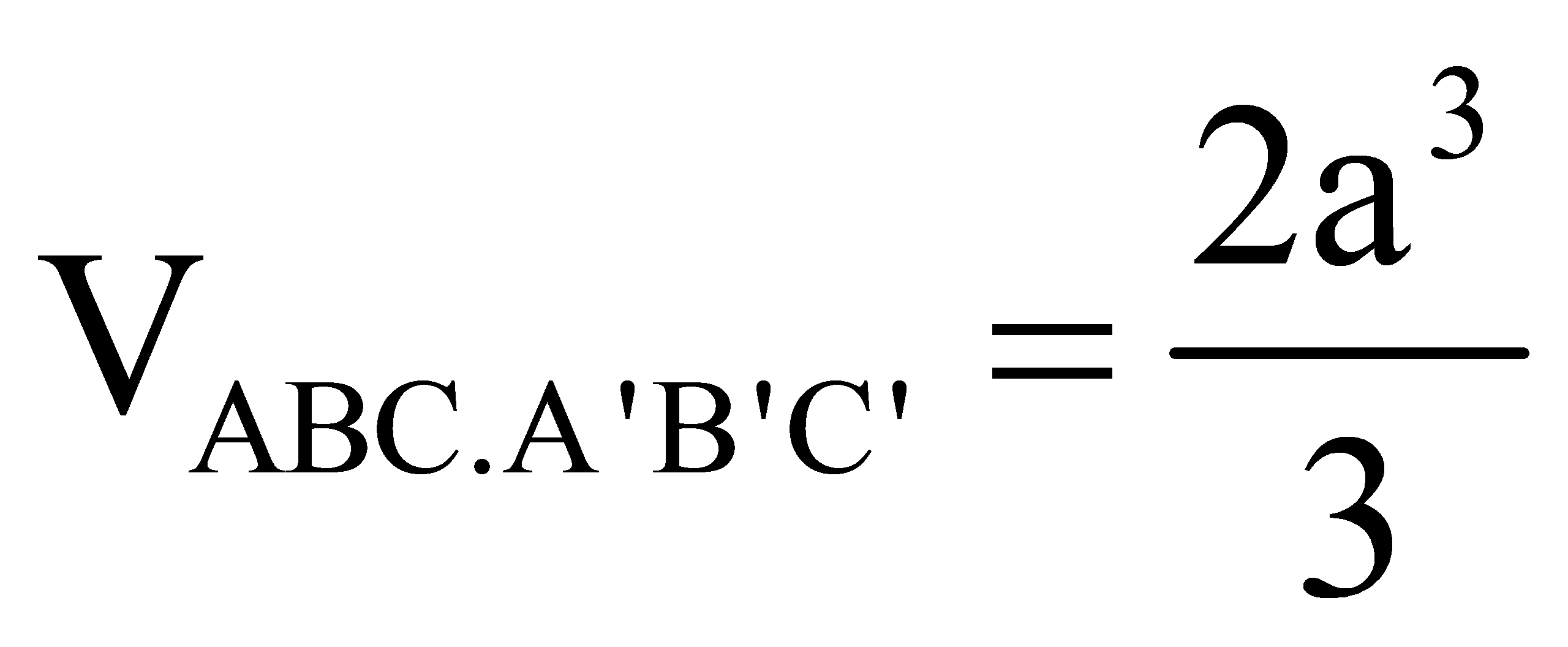 .
.
C.
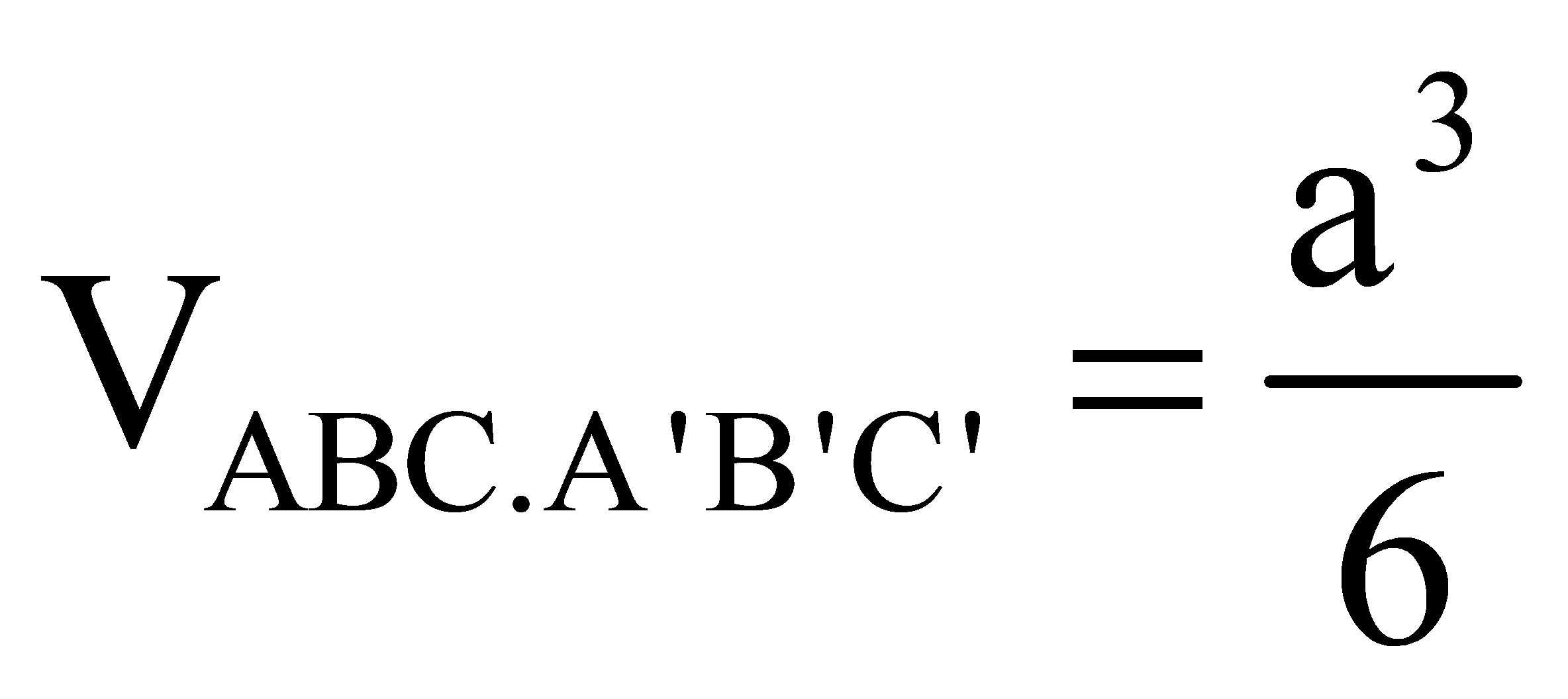 .
.
D.
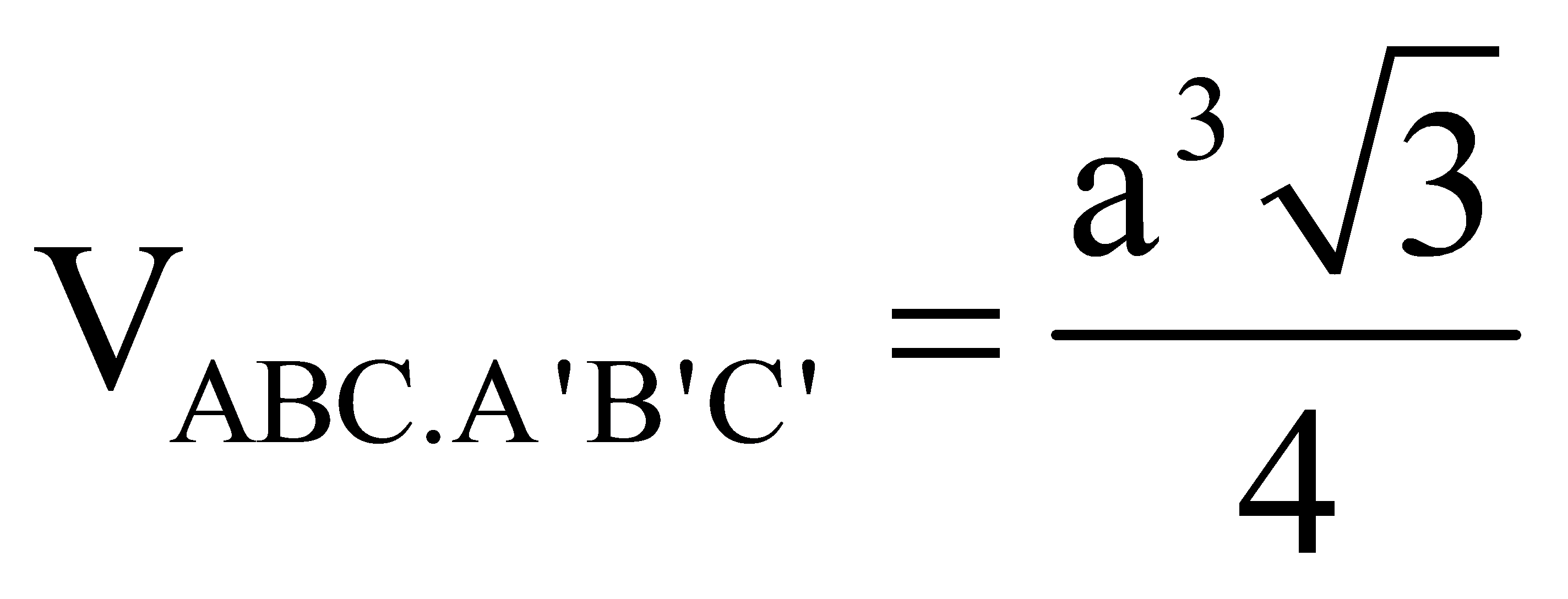 .
.
Đáp án và lời giải
Đáp án:D
Lời giải:
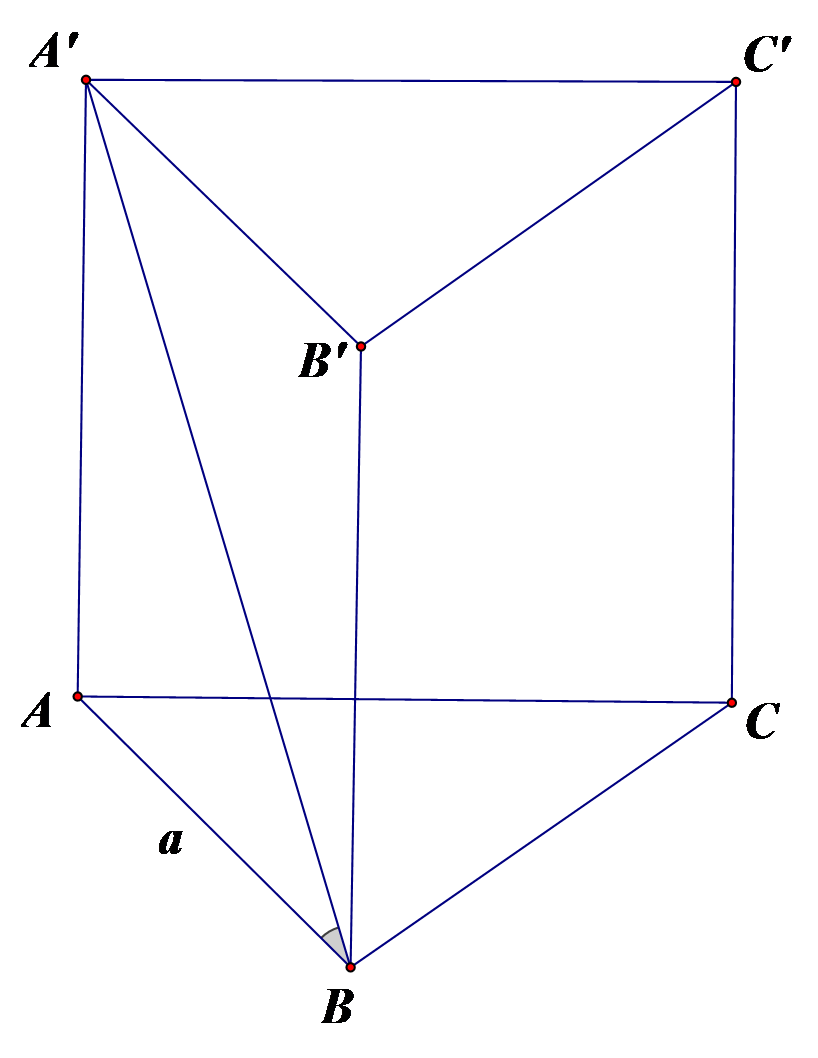
Tam giác ABC đều: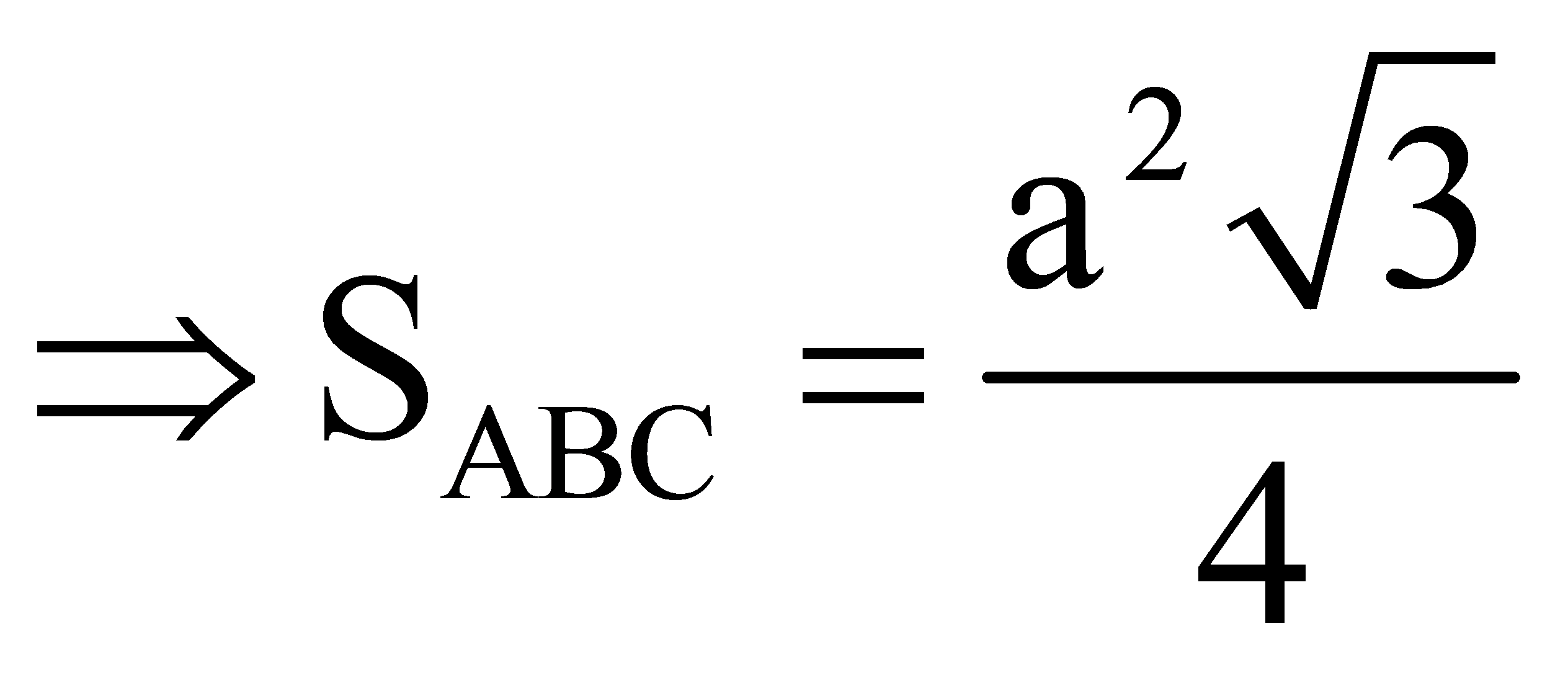
Góc giữa ![]() vuông cân tại A
vuông cân tại A
![]()
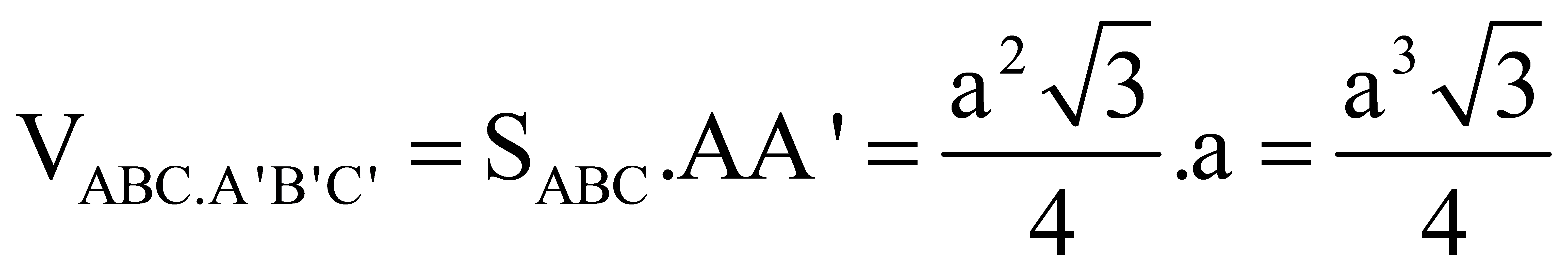 (đvtt).
(đvtt).
Vậy đáp án đúng là: D.
Câu hỏi thuộc đề thi sau. Bạn có mong ước thi thử?
Bài tập trắc nghiệm 60 phút Thể tích khối lăng trụ. - Khối đa diện và thể tích - Toán Học 12 - Đề số 9
Làm bài
Chia sẻ
Một số thắc mắc khác cùng bài thi.
Khối lăng trụ ABC.A’B’C’ hoàn toàn có thể tích bằng ![]() , đáy là tam giác đều cạnh bằng 2a. Tính khoảng chừng cách giữa AB và B’C’.
, đáy là tam giác đều cạnh bằng 2a. Tính khoảng chừng cách giữa AB và B’C’.
Cho lăng trụ đứng ![]() có đáy là tam giác đều cạnh
có đáy là tam giác đều cạnh ![]() . Đường thẳng
. Đường thẳng ![]() phù phù hợp với đáy một góc
phù phù hợp với đáy một góc ![]() . Tính thể tích
. Tính thể tích ![]() của khối lăng trụ
của khối lăng trụ ![]() .
.
Cho lăng trụ đứng ![]() có đáy là tam giác đều cạnh
có đáy là tam giác đều cạnh ![]() . Mặt phẳng
. Mặt phẳng ![]() tạo với mặt đáy góc
tạo với mặt đáy góc ![]() . Tính theo
. Tính theo ![]() thể tích khối lăng trụ
thể tích khối lăng trụ ![]() .
.
Cho lăng trụđứng ![]() có đáy
có đáy ![]() là tam giác đều cạnh bằng
là tam giác đều cạnh bằng ![]() . Cạnh bên
. Cạnh bên ![]() . Thểtích khối lăng trụ
. Thểtích khối lăng trụ![]() là
là
Cho một tấm nhôm hình chữ nhật ![]() có
có ![]() ,
, ![]() . Ta gập tấm nhôm theo hai cạnh
. Ta gập tấm nhôm theo hai cạnh ![]() và
và ![]() vào phía trong cho tới lúc
vào phía trong cho tới lúc ![]() và
và ![]() trùng nhau như hình vẽ bên để dược một hình lăng trụ khuyết hai đáy. Khi đó hoàn toàn có thể tạo được khối lăng trụ với thể tích lớn số 1 bằng:
trùng nhau như hình vẽ bên để dược một hình lăng trụ khuyết hai đáy. Khi đó hoàn toàn có thể tạo được khối lăng trụ với thể tích lớn số 1 bằng:
Lăng trụ đứng ABC.A’B’C’ có đáy là tam giác vuông cân tại A, ![]() , cạnh bên
, cạnh bên ![]() và có hai đáy là hai tam giác nội tiếp hai đường tròn đáy của hình trụ
và có hai đáy là hai tam giác nội tiếp hai đường tròn đáy của hình trụ ![]() . Tính thể tích khối trụ
. Tính thể tích khối trụ ![]() .
.
Lăng trụ đứng ABCA’B’C’ có đáy là tam giác vuông cân AB = AC = a, A’C = 2a. Thể tích khối trụ là
Cho khối lăng trụ đứng tam giác ![]() có đáy là một tam giác vuông cân tại
có đáy là một tam giác vuông cân tại ![]() ,
, ![]() , góc giữa
, góc giữa ![]() và mặt phẳng
và mặt phẳng ![]() bằng
bằng ![]() . Thể tích khối lăng trụ
. Thể tích khối lăng trụ ![]() là
là
Một hình hộp chữ nhật có kích thước a (cm) x b (cm) x c (cm) , trong đó a, b , c là những số nguyên và 1≤a≤b≤c . Gọi V (cm3) và S (cm2) lần lượt là thể tích và diện tích s quy hoạnh toàn phần của hình hộp. Biết V=S , tìm số những bộ ba số (a,b,c) ?
Cho hình lập phương ABCD.A’B’C’D’, có cạnh bằng 3, và hình nón có đỉnh O, đường tròn đáy có bán kính là O’A’ (như hình vẽ bên). Tính tỉ số ![]() , biết rằng V1 là thể tích của hình lập phương và V2 là thể tích của hình nón.
, biết rằng V1 là thể tích của hình lập phương và V2 là thể tích của hình nón.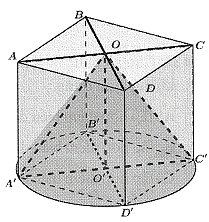
Các đường chéo của những mặt một hình hộp chữ nhật bằng ![]() Tính thể tích
Tính thể tích ![]() của khối hộp chữ nhật đó.
của khối hộp chữ nhật đó.
Cho hìnhhộpđứng![]() cóđáylàhìnhvuông, cạnhbênbằng
cóđáylàhìnhvuông, cạnhbênbằng![]() vàđườngchéo
vàđườngchéo![]() . Thểtích
. Thểtích![]() củakhốihộp
củakhốihộp![]() bằngbaonhiêu?
bằngbaonhiêu?
Tính thể tích ![]() của khối hộp chữ nhật
của khối hộp chữ nhật ![]() , biết
, biết ![]()
Lăng trụ đứng ABCA’B’C’ có đáy là tam giác vuông cân AB = AC = a, A’C = 2a. Thể tích khối trụ là ?
Xét một hộp bóng bàn có dạng hình hộp chữ nhật. Biết rằng hộp chứa vừa khít ba quả bóng bàn được xếp theo chiều dọc, những quả bóng bàn có kích thước như nhau. Phần không khí còn trống trong hộp chiếm
Cho khối lăng trụ (T) có độ cao bằng a và thể tích bằng ![]() Tính diện tích s quy hoạnh đáy S của (T).
Tính diện tích s quy hoạnh đáy S của (T).
Lăng trụ đứng ![]() có đáy là tam giác đều cạnh a, cạnh bên độ dài
có đáy là tam giác đều cạnh a, cạnh bên độ dài ![]() . Thể tích khối trụ là ?
. Thể tích khối trụ là ?
Cho lăng trụ tam giác đều ![]() có tất cả những cạnh đều bằng
có tất cả những cạnh đều bằng ![]() . Tính thể tích của khối lặng trụ.
. Tính thể tích của khối lặng trụ.
Cho hình lập phương cạnh a và một hình trụ có hai đáy là hai hình tròn trụ nội tiếp hai mặt đối diện của hình lập phương. Gọi![]() là diện tích s quy hoạnh của sáu mặt của hình lập phương,
là diện tích s quy hoạnh của sáu mặt của hình lập phương, ![]() là diện tích s quy hoạnh xung quanh của hình trụ. Tỉ số
là diện tích s quy hoạnh xung quanh của hình trụ. Tỉ số![]() bằng ?
bằng ?
Cho lăng trụ xiên tam giác ABC.A'B'C' có đáy ABC là tam giác đều cạnh a . Hình chiếu của A' xuống (ABC) là tâm O đường tròn ngoại tiếp tam giác ABC biết AA' phù phù hợp với đáy ABC một góc 60 . Tính thể tích khối lăng trụ.
Cho lăng trụ đứng ![]() có đáy
có đáy ![]() là tam giác vuông tại
là tam giác vuông tại ![]() ;
; ![]() ;
; ![]() . Biết cạnh bên của lăng trụ bằng
. Biết cạnh bên của lăng trụ bằng ![]() . Thể tích khối lăng trụ là:
. Thể tích khối lăng trụ là:
Cho hình lăng trụđứng ![]() cóđáy là hình vuông vắn cạnh bằng 3, đường chéo
cóđáy là hình vuông vắn cạnh bằng 3, đường chéo ![]() của mặt bên
của mặt bên ![]() cóđộ dài bằng 5. Tính thể tích V của khối lăng trụ
cóđộ dài bằng 5. Tính thể tích V của khối lăng trụ![]()
Cho khối lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác đều cạnh 2a, gọi I là trung điểm BC, góc giữa A’I và mặt phẳng (ABC) bằng ![]() . Thể tích của khối lăng trụ ABC.A’B’C’ là:
. Thể tích của khối lăng trụ ABC.A’B’C’ là:
Cho hình chóp S.ABCD có đáy ABCD là hình thang với hai cạnh đáy là AD và BC trong đó ![]() , AC cắt BD tại O, thể tích khối chóp S.OCD là
, AC cắt BD tại O, thể tích khối chóp S.OCD là ![]() , khi đó thể tích khối chóp S.ABCD là:
, khi đó thể tích khối chóp S.ABCD là:
Diện tích toàn phần của một hình lập phương bằng ![]() .Thể tích khối lập phương đó :
.Thể tích khối lập phương đó :
Cho khốilăngtrụđứng![]() cóđáylàtam giácđều. Mặtphẳng
cóđáylàtam giácđều. Mặtphẳng![]() tạovớiđáygóc
tạovớiđáygóc![]() vàtam giác
vàtam giác![]() códiệntíchbằng8.TínhthểtíchVcủakhốilăngtrụđãcho.
códiệntíchbằng8.TínhthểtíchVcủakhốilăngtrụđãcho.
Cho hình lăng trụ đứng ![]() có đáy ABC là tam giác vuông tại A,
có đáy ABC là tam giác vuông tại A, ![]() . Đuòng chéo B’C của mặt bên (BB’C’C) tạo với mặt phẳng (AA’C’C) một góc 30. Tính thể tích của khối lăng trụ theo a.
. Đuòng chéo B’C của mặt bên (BB’C’C) tạo với mặt phẳng (AA’C’C) một góc 30. Tính thể tích của khối lăng trụ theo a.
Cho lăng trụ ![]() có đáy
có đáy ![]() là hình thoi cạnh
là hình thoi cạnh ![]() , biết
, biết ![]() là hình chóp đều và
là hình chóp đều và ![]() phù phù hợp với mặt đáy một góc
phù phù hợp với mặt đáy một góc ![]() . Thể tích khối lăng trụ
. Thể tích khối lăng trụ ![]() là:
là:
Cho hình lăng trụ ![]() có đáy
có đáy ![]() là hình thoi cạnh a,
là hình thoi cạnh a, ![]() . Chân đường cao hạ từ B’ trùng với tâm O của đáy
. Chân đường cao hạ từ B’ trùng với tâm O của đáy ![]() ; góc giữa mặt phẳng
; góc giữa mặt phẳng ![]() với đáy bằng 60. Thể tích lăng trụ bằng:
với đáy bằng 60. Thể tích lăng trụ bằng:
Cho hình hộp đứng ![]() có đáy là hình vuông vắn, cạnh bên bằng
có đáy là hình vuông vắn, cạnh bên bằng ![]() và đường chéo
và đường chéo ![]() . Tính thể tích khối hộp này.
. Tính thể tích khối hộp này.
Cho một hình hộp chữ nhật. Nếu ta tăng độ cao của hình hộp lên 6 lần và giảm những kích thước đáy 3 lần thì thể tích khối hộp thay đổi ra làm sao?
Cho một khối trụ có bán kính đáy bằng a, thiết diện của hình trụ qua trục là hình vuông vắn cóchu vi là 8. Thể tích khối trụ có mức giá trị bằng:
Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a, cạnh bên A’B tạo với đáy một góc 45. Thể tích khối lăng trụ ABC.A’B’C’ là:
Tính thể tích V của khối lăng trụ có diện tích s quy hoạnh mặt đáy bằng ![]() và độ cao bằng
và độ cao bằng ![]()
Cho khối lăng trụ đứng ![]() có đáy
có đáy ![]() là tam giác cân với
là tam giác cân với ![]() ,
, ![]() . Mặt phẳng
. Mặt phẳng ![]() tạo với đáy một góc
tạo với đáy một góc ![]() . Tính thể tích
. Tính thể tích ![]() của khối lăng trụ đã cho.
của khối lăng trụ đã cho.
Đáy của lăng trụ đứng tam giác ![]() là tam giác đều cạnh
là tam giác đều cạnh ![]() . Mặt
. Mặt ![]() tạo với đáy một góc 30 và diện tích s quy hoạnh tam giác
tạo với đáy một góc 30 và diện tích s quy hoạnh tam giác ![]() bằng 8. Tính thể tích khối lăng trụ.
bằng 8. Tính thể tích khối lăng trụ.
Cho khối lăng trụ tam giác đều ABC.A’B’C’. Gọi M là trung điểm cạnh AA’. Mặt phẳng (MBC) chia khối lăng trụ thành hai phần. Tỉ số thể tích cua hai phần đó bằng:
Cho lăng trụđứng ABC.A’B’C’ cóđáy ABC là tam giác vuông cân tại B. Biết ![]() . Thể tích khối lăng trụđã cho là
. Thể tích khối lăng trụđã cho là
Cho hình lăng trụ tam giác đều ![]() có
có ![]() ,
, ![]() . Tính thể tích khối lăng trụ
. Tính thể tích khối lăng trụ ![]() .
.
Cho hình lăng trụ ![]() . Gọi
. Gọi ![]() ,
, ![]() ,
, ![]() lần lượt là những điểm thuộc những cạnh
lần lượt là những điểm thuộc những cạnh ![]() ,
, ![]() ,
, ![]() sao cho
sao cho ![]() ,
, ![]() ,
, ![]() . Gọi
. Gọi ![]() ,
, ![]() lần lượt là thể tích của hai khối đa diện
lần lượt là thể tích của hai khối đa diện ![]() và
và ![]() . Tính tỉ số
. Tính tỉ số ![]() .
.
Một số thắc mắc khác hoàn toàn có thể bạn quan tâm.
Cho hình hộp chữ nhật ![]() có
có ![]() . Gọi M, N, P lần luợt là trung điểm những cạnh
. Gọi M, N, P lần luợt là trung điểm những cạnh ![]() và
và ![]() (tham khảo hình vẽ bên). Côsin góc giữa hai mặt phẳng
(tham khảo hình vẽ bên). Côsin góc giữa hai mặt phẳng ![]() và
và ![]() bằng:
bằng: 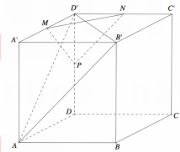
Cho một lượng rất nhỏ bột sắt vào dung dịch HCl dư thu được dung dịch (A) và khí (B). Sau đó cho tiếp dung dịch AgNO3 dư vào dung dịch (A) thì thu được dung dịch (D) và chất rắn (E). Biết những phản ứng xẩy ra hoàn toàn, số chất trong dung dịch (D) (không tính nước) và chất rắn (E) lần lượt là ?
Cho vậtđượcđỡbởihaithanhnhưhìnhvẽ. Biếtgiatốctrọngtrườngg = 10 m/s2vàcácphảnlựcdo thanhtácdụnglênvậthướngdọctheothanh. Lựcdo thanh(1) tácdụnglênvậtlà50 N. Khốilượngcủavậtlà: 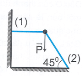
Trong hệ trục tọa độ![]() cho hai điểm
cho hai điểm ![]() và đường thẳng
và đường thẳng 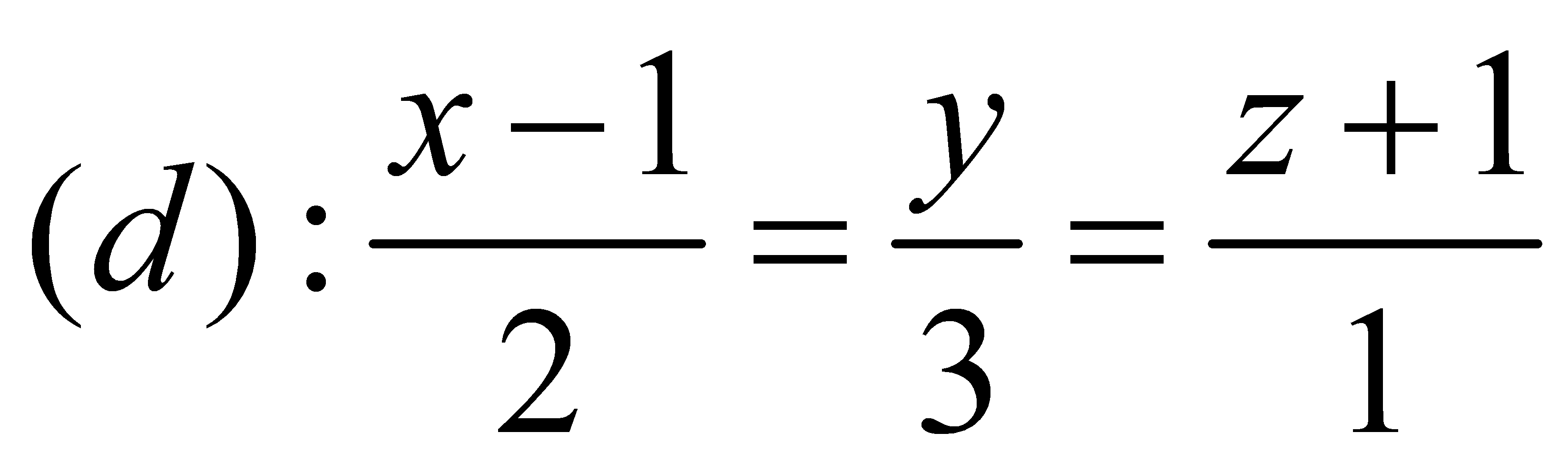 .Tìm điểm
.Tìm điểm ![]() trên đường thẳng
trên đường thẳng ![]() sao cho tam giác
sao cho tam giác ![]() nhỏ nhất .
nhỏ nhất .
Giá trị lớn số 1 của hàm số 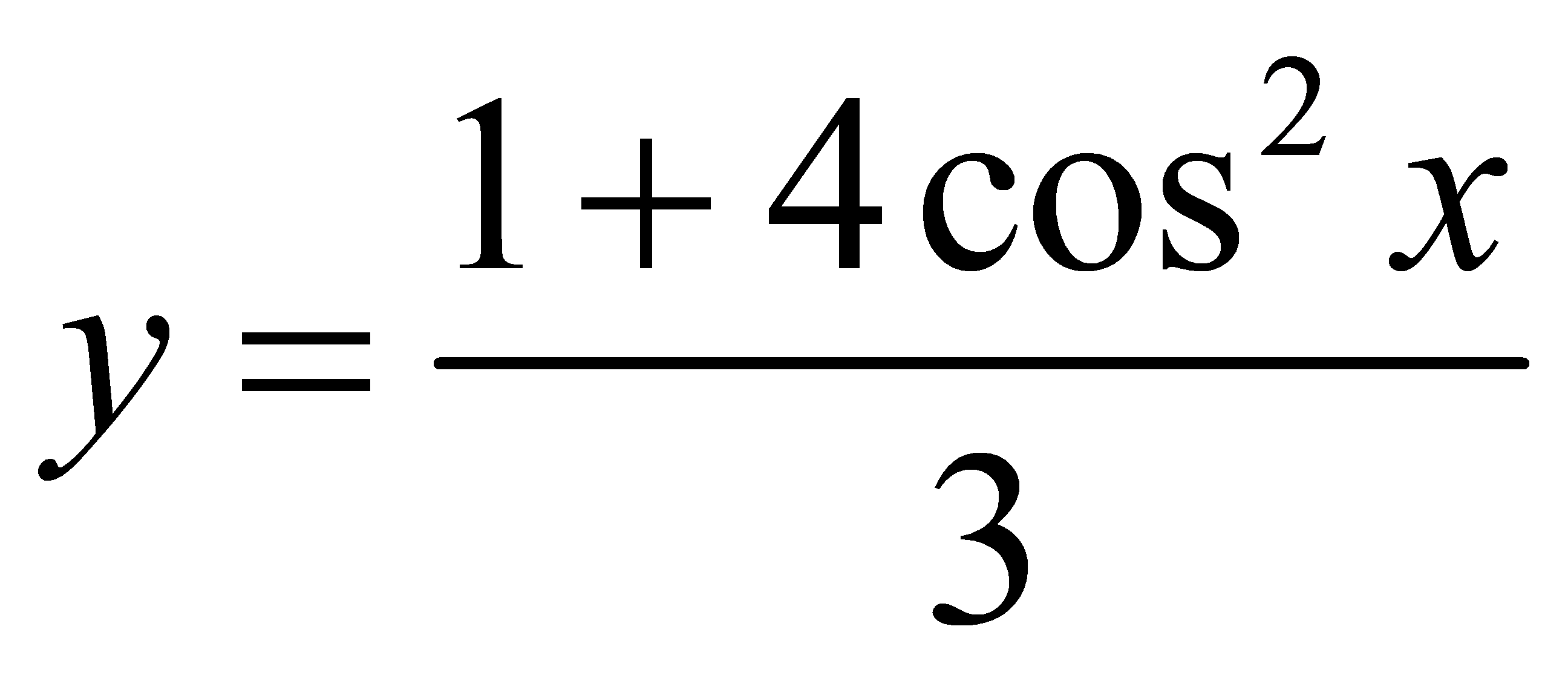 đạt được khi:
đạt được khi:
Cho một tấm tôn hình chữ nhật ABCD có ![]() . Ta gập tấm tôn theo 2 cạnh MN và QP vào phía trong sao cho BA trùng với CD để được lăng trụ đứng khuyết hai đáy. Khối lăng trụ có thể tích lớn nhất khi
. Ta gập tấm tôn theo 2 cạnh MN và QP vào phía trong sao cho BA trùng với CD để được lăng trụ đứng khuyết hai đáy. Khối lăng trụ có thể tích lớn nhất khi ![]() bằng bao nhiêu?
bằng bao nhiêu? 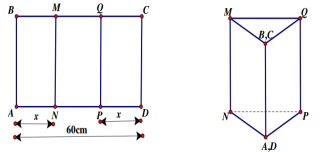
Hàm số ![]() đồng biến trên:
đồng biến trên:
Tiếp tuyến của đồ thị hàm số![]() tại điểm
tại điểm 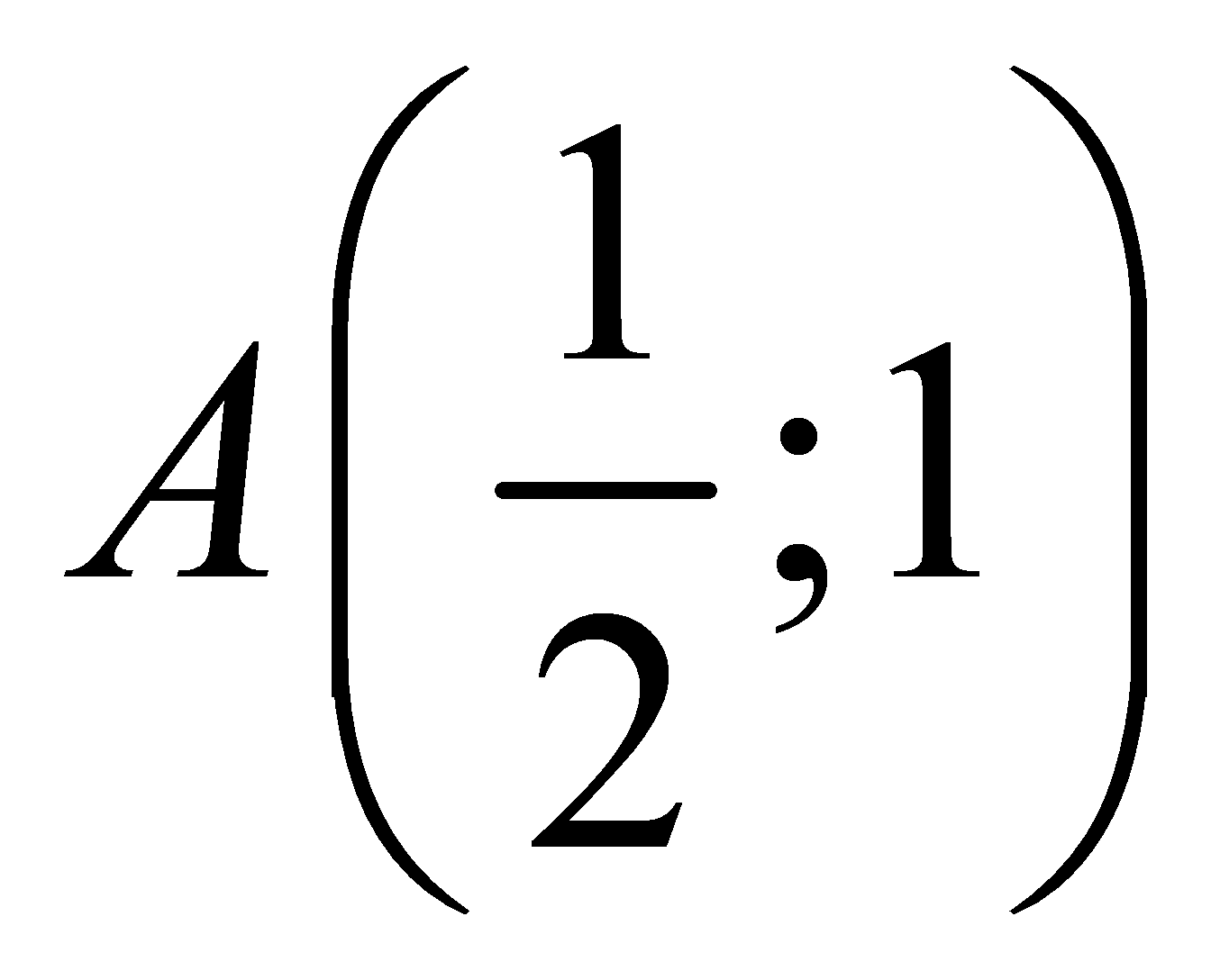 có phương trình:
có phương trình:
Tiến hành bốn thí nghiệm sau:
- Thí nghiệm 1: Nhúng thanh Fe vào dung dịch FeCl3;
- Thí nghiệm 2: Nhúng thanh Fe vào dung dịch CuSO4;
- Thí nghiệm 3: Nhúng thanh Cu vào dung dịch FeCl3;
- Thí nghiệm 4: Cho thanh Fe tiếp xúc với thanh Cu rồi nhúng vào dung dịch HCl.
Số trường hợp xuất hiện ăn mòn điện hoá là
Đung nóng 100 gam dung dịch Glucozơ 18% với lượng dư dung dịch AgNO3 trong NH3 đến khi phản ứng xảy ra hoàn toàn thu được m gam Ag. Giá trị của m là:
